
위 질문이 성립하지 않는다는 사실은 모두 쉽게 인정(?) 하였지만
신박하고 새로운 방법으로 설명한 학생은 찾기 어려웠습니다.
루트2의 대략적인 값에 주목하는 현상만 보이고, 기대했던 그림으로 표현하는 학생은 기다려도 좀처럼 등장하지 않아 아쉬움이 있었습니다.
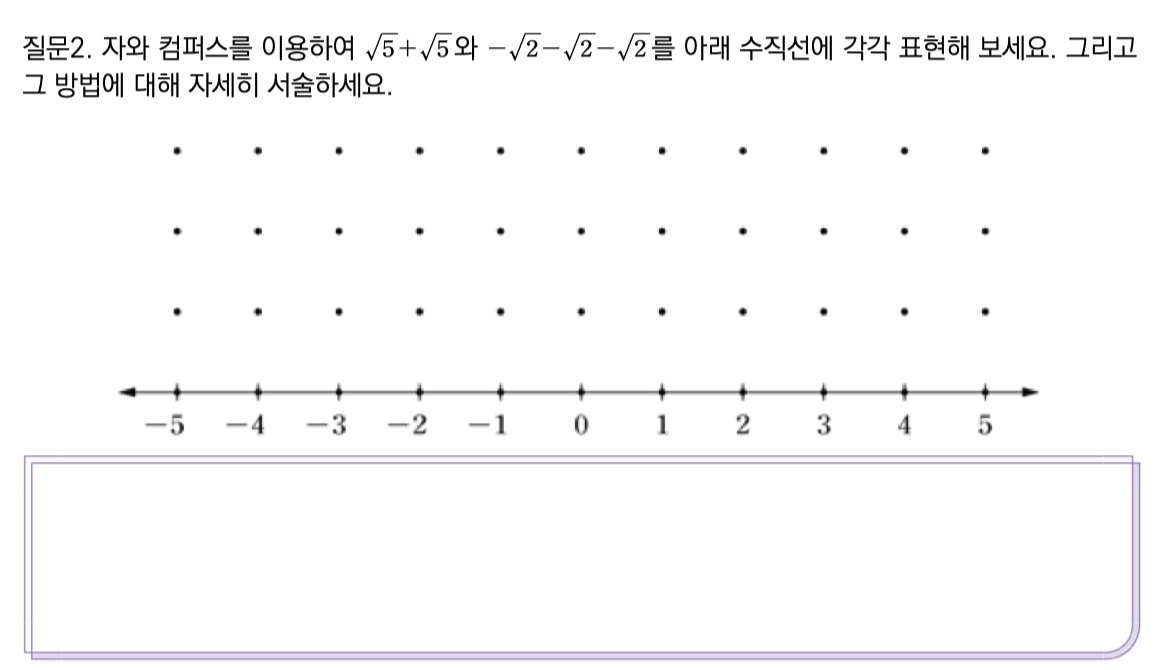
컴퍼스를 이용하여 그리는건 역시 좋은거 같습니다.
우선 수직선에 대한 이해가 깊어집니다.
그리고 원래 목표로 했던 루트안의 수가 다르면 도저히 간단히 할 수 없다는 것을 조금은 이해하게 됩니다.
앞선 질문1과도 연결되어 덧셈의 원리에 대해 직관적으로 이해하며, 제곱근의 덧셈의 원리에 대해 알게 되는 활동이었습니다.
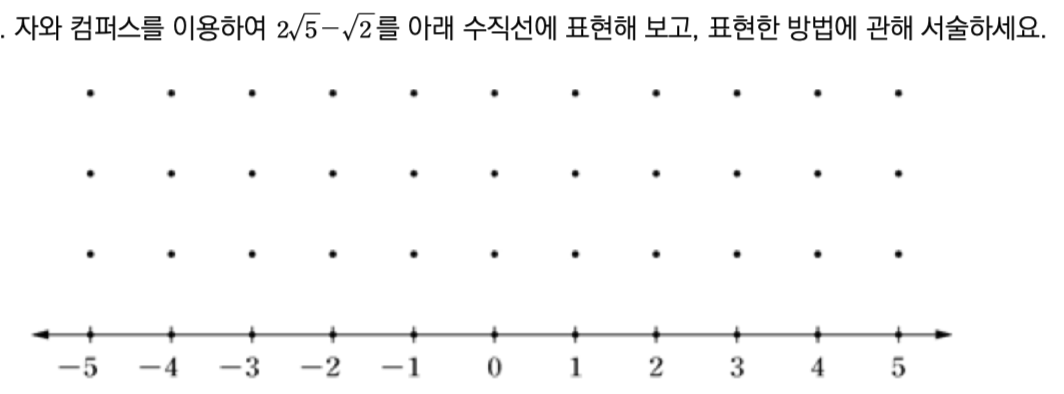
이문제는 의외의 질문이 재미있게 진행되었습니다.
컴퍼스로 그리면 거의 3에 찍힙니다.
실제로 값은 3.05쯤으로 3에서 아주 살짝 오른쪽에 찍혀야 합니다.
하지만 컴퍼스로 옮기는 과정에서의 오류가 있을 수 있어 3의 왼쪽인지 오른쪽인지 확인하기 어렵습니다.
그래서 3보다 큰지 작은지 확인해 보라고 요구하였고,
이는 쉽지 않은 문제입니다.
소수점 2째자리 정도 까지의 근사값을 구해야 해결할 수 있는 문제가 되고 이는 지난 시간에 소수좀 아래 숫자를 10번째 자리까지 구해본 경험이 해결에 도움이 되었습니다.
아직 수업을 안하셨다면 한 번 비교해보게 해보시는것도 좋을거 같습니다
"제곱근의 덧셈과 뺄셈을 그림으로 표현하면서 직관적으로 이해하는 것이 정말 흥미로운 활동이었네요. 컴퍼스를 이용하여 수학적인 개념을 시각적으로 표현하는 것은 학습에 큰 도움이 될 것 같아요. 이러한 활동을 통해 수학을 더욱 재밌게 다가갈 수 있죠. 계속해서 창의적인 학습 방법을 모색해 나가면 좋을 것 같습니다!"